ResumosMIEI

Uma coleção de resumos, para ajudar os que precisam daquele empurrão.

---

Project maintained by mendess Hosted on GitHub Pages — Theme by mattgraham

Introdução a Haskell

Uma função em Haskell tem bastantes semelhaças com um função matematica.

Por exemplo:

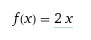
em Haskell seria:

f x = 2 * x

Tipos

Em Haskell são muito importantes os tipos das funções, por exemplo, o tipo da função anterior seria:

f :: Int -> Int

isto indica-nos que a função tem como input um Int (numero inteiro) e como output outro Int.

Outros tipos importantes a saber são:

• Float: Números reais
• Bool: False ou True
• Char: Caracteres ('a', 'b', etc)
• [a]: Lista de a. Esta pode ser uma lista de qualquer coisa, se quisermos ser especificos podemos usar [Int] para uma lista de Ints.
• String: Texto. Este é equivalente a escrever [Char] porque texto é apenas uma lista de caracteres.

Podemos ainda definir novos tipos. Há dois metodos para isto:

A keyword type permite definir um alias para outro tipo.

type Hora = (Int,Int)

Assim, escrever Hora ou (Int,Int) é equivalente mas o primeiro mostra alguma intenção, ou seja, uma função que receba uma Hora diz-nos que irá intrepertar o par como (Horas, Minutos).

A keyword data permite definir um novo tipo de dados

data Hora = H Int Int

Isto irá ser aprofundado mais a frente.

Operadores

Os operadores que podemos usar são os mesmos da matemática: +, -, * e / para operações aritemeticas mais os operadores lógicos:

• > <: maior e menor
• >= <=: maior ou igual e menor ou igual
• ==: Igualdade

Estruturas de controlo

Em certas ocasiões um função pode ter de fazer um processamento mais complexo do seu input.

Por exemplo a função seguinte:

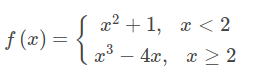
em Haskell fica

f :: Int -> Int
f x | x < 2  = x^2 + 1
    | x >= 2 = x^3 - 4 * x

A isto chamam-se guardas. É possível acrescentar um caso no fim da guarda que executa caso nenhuma das condições seja satisfeita.

f :: Int -> Int
f x | x < 0     = x^2 + 1
    | x == 0    = x
    | otherwise = x^3

Para além destas podemos ainda usar if then else apesar de este não ser tão legivel:

f :: Int -> Int
f x = if x < 2 then x^2 + 1 else x^3 - 4 * x

Pattern matching

Podemos também tratar o input de uma função com pattern matching, por exemplo, para definir a negação lógica ( ¬ ) podemos fazer a seguinte função.

negacao :: Bool -> Bool
negacao False = True
negacao True = False

Isto quer dizer que sempre que a função recebe um False devolve um True e vice versa.

Outra forma de fazer isto é com um case:

negacao :: Bool -> Bool
negacao x = case x of
            False -> True
            True -> False

Pattern matching pode ser aplicado para todos os tipos de dados, como iremos ver noutros resumos.

Exemplos de funções

perimetro :: Float -> Float
perimetro r = 2 * 3.14 * r

soma :: Int -> Int -> Int
soma a b = a + b

type Hora = (Int,Int)

avancaUmaHora :: Hora -> Hora
avancaUmaHora (23,m) = (0,m)
avancaUmaHora (h,m)  = (h + 1, m)

data Hora = H Int Int

avancaUmaHora :: Hora -> Hora
avancaUmaHora (H 23 m) = H 0 m
avancaUmaHora (H h m) = H (h + 1) m